заочный тур:
условия в формате HTML или
в формате PDF (140КБ),
English version is available PDF (140K)
решения в формате PDF (250КБ),
English version is available PDF (230K),
список участников финального тура
финальный тур:
расписание (русская версия, english version),
условия задач в формате html,
условия и решения задач в формате PDF (200КБ),
English version is available PDF (200КБ),
Лекция А.А.Заславского "Еще раз о задаче Мальфатти" PDF (340КБ)
победители финального тура,
учителя геометрии участников финального тура,
фотогалерея олимпиады
В память о выдающемся деятеле российского математического образования,
всемирно известном знатоке и патриоте элементарной геометрии
Игоре Федоровиче Шарыгине (1937–2004)
Математический институт им В.А. Стеклова РАН,
Департамент образования города Москвы,
Московский центр непрерывного математического образования,
Московский институт открытого образования,
Открытый лицей ВЗМШ,
при поддержке
компьютермаркета «НИКС» и
АНО «Школа нового поколения»,
уже пятый год проводят геометрическую олимпиаду. В оргкомитет и жюри олимпиады
входят известные ученые, педагоги, энтузиасты математического просвещения
из разных российских регионов.
С 2006 года олимпиада проходит при информационной
поддержке газеты «Математика».
Финальный тур олимпиады прошёл в Дубне 29 июля – 1 августа 2009 года, олимпиада была двухдневной (как и в прошлом году).
В ней приняли участие 55 школьников из России, Украины, Молдавии, Армении, Болгарии и Румынии.
Жюри и оргкомитет олимпиады также хотят сказать спасибо тем, что обычно в таких случаях
остается в тени – учителям геометрии,
которые учат всех тех, кто принял участие в финальном туре олимпиады!
8 класс
I диплом
Скутин Александр, г. Москва, лицей "Вторая школа"
Иванов Константин, г. Москва, школа 25
II диплом
Крачун Дмитрий, г. Санкт-Петербург, лицей 239
Хилько Данил, г. Киев, лицей 208
Сандрикова Мария, г. Москва, ЦО 218
Кузин Михаил, г. Москва, школа 25
Недошивин Михаил, г. Санкт-Петербург, лицей 239
III диплом
Лузин Игорь, г. Москва, лицей "Вторая школа"
Кленин Егор, г. Москва, лицей "Вторая школа"
Максаев Артём, г. Москва, лицей "Вторая школа"
Рудых Василиса, г. Якутск, Республиканский лицей
Косинов Никита, г. Ульяновск, школа 20
Нови-Окли Владислав, г. Ярославль, гимназия 3
Матвеевский Дмитрий, г. Харьков, школа 27
Грамотами за успешное выступление награждены:
Рябцева Мария, г. Ульяновск, школа 79
Соскин Даниэл, г. Киев, Русановский лицей
Адимов Арсений, г. Ростов-на-Дону, лицей 1 Классический
Горелов Иван, г. Москва, школа 25
Южаков Александр, г. Курган, школа 31
9 класс
I диплом
Малясова Виктория, г. Ростов-на-Дону, "Экономический лицей" 14
II диплом
Егоров Дмитрий, г. Санкт-Петербург, лицей 239
III диплом
Мукосеева Екатерина, г. Санкт-Петербург, ФМЛ 30
Барановский Александр, г. Киев, Русановский лицей
Макаров Даниил, г. Москва, гимназия 1543
Осипов Матвей, г. Ульяновск, школа 20
Грамотами за успешное выступление награждены:
Бурова Ольга, г. Москва, лицей "Вторая школа"
Иванов Андрей, г. Кишинёв (Молдавия), Теоретический лицей "Оризонт"
Ионов Андрей, г. Москва, школа 57
Гулин Всеволод (8 класс), г. Харьков, "Академическая гимназия" 45
Миронов Михаил, г. Москва, школа 57
10 класс
I диплом
Омельяненко Виктор, г. Белгород, школа 38
II диплом
Ивлев Фёдор, г. Москва, СУНЦ МГУ
Машников Олег, г. Курган, школа 42
Ерохин Станислав, г. Санкт-Петербург, ФМЛ 239
Савенков Кирилл, г. Санкт-Петербург, ФМЛ 239
III диплом
Климовицкий Иосиф, г. Санкт-Петербург, ФМЛ 239
Бояров Игорь, г. Тольятти, школа 51
Устинов Никита, г. Санкт-Петербург, ФМЛ 239
Вълков Младен, г. Шумен (Болгария), школа "Нанчо Попович"
- CIOLAN EMIL
- Белухов Николай
- Берлов Сергей Львович
- Берштейн Александр Лазаревич
- Блинков Александр Давидович
- Бочанова Наталья Владимировна
- Бутузов Валентин Федорович
- Бухтояров Владимир Владимирович
- Васянин Сергей Иванович
- Васянина Анна Викторовна
- Волчкевич Максим Анатольевич
- Воробьев Андрей Юрьевич
- Гордин Рафаил Калманович
- Дольников Владимир Леонидович
- Ефимов Андрей Михайлович
- Ефимова Инна Валерьевна
- Жижилкин Игорь Дмитриевич
- Иванова Елена Юрьевна
- Ицыксон Дмитрий Михайлович
- Калинин Дмитрий Александрович
- Карпов Дмитрий Валерьевич
- Кирлица Александр Вячеславович
- Ковальджи Александр Кириллович
- Кожевников Павел Александрович
- Кошина Наталья Трифоновна
- Крыжановский Александр Феликсович
- Кысылбаиков Илья Гаврилович
- Лифиц Сергей Александрович
- Лычева Валентина Арсентьевна
- Маргарян Тигран
- Мухина Галина Геннадьевна
- Ниренбург Татьяна Леонидовна
- Оскорбин Дмитрий Николаевич
- Пастор Алексей Владимирович
- Пратусевич Максим Яковлевич
- Преображенский Игорь Евгеньевич
- Ростовский Дмитрий Андреевич
- Сагай Елена Николаевна
- Самойлов Леонид Михайлович
- Сгибнев Алексей Иванович
- Соломин Вадим Николаевич
- Телеукэ Марчел
- Тимошкевич Виктория Алексеевна
- Тимошкевич Тарас Дмитриевич
- Филатов Егор Константинович
- Филипповский Григорий Борисович
- Харик Елена Ефимовна
- Ходзицкая Елена Александровна
- Шамович Александр Анатольевич
- Шарич Владимир Златкович
- Южаков Олег Иванович
- Юрьев Денис
8 класс.
Первый день.
1. В трапеции ABCD боковая сторона AB равна меньшему
основанию BC, а диагональ AC равна основанию AD. Прямая, проходящая через
вершину B параллельно AC, пересекает прямую DC в точке M. Докажите, что
AM — биссектриса угла BAC.
2. Через точку внутри вписанного четырехугольника провели две прямые,
делящие его на четыре четырехугольника. Три из этих четырехугольников — вписанные,
причем радиусы описанных вокруг них окружностей равны. Докажите, что
четвертая часть — четырехугольник, вписанный в окружность того же радиуса.
3. Пусть AHa и BHb — высоты треугольника ABC, P и Q —
проекции точки Ha на стороны AB и AC. Докажите, что прямая PQ делит отрезок
HaHb пополам.
4. В треугольнике ABC угол A равен 57o,
угол B равен 61o, угол C равен 62о. Какой
из двух отрезков длиннее: биссектриса угла A или медиана, проведенная из вершины
B?
Второй день.
5. Из вершины B треугольника ABC опущен перпендикуляр BM на
биссектрису угла C. Пусть K — точка касания вписанной окружности со стороной BC.
Найдите угол MKB, если известно, что угол BAC равен a.
6. Можно ли расположить на плоскости четыре равных многоугольника
так, чтобы любые два из них не имели общих внутренних точек, но имели общий
отрезок границы?
7. Вокруг треугольника ABC описали окружность s. Пусть L и W —
точки пересечения биссектрисы угла A со стороной BC и окружностью s соответственно.
Точка O — центр описанной окружности треугольника ACL. Восстановите
треугольник ABC, если даны окружность s и точки W и O.
8. Вписанная и вневписанная окружности треугольника ABC
касаются стороны BC в точках M и N. Известно, что угол BAC в два раза больше угла MAN. Докажите,
что BC = 2MN.
9 класс.
Первый день.
1. Середина стороны треугольника и основание высоты,
проведенной к этой стороне, симметричны относительно точки касания этой стороны
с вписанной окружностью. Докажите, что эта сторона составляет треть периметра
треугольника.
2. Дан выпуклый четырехугольник ABCD. Обозначим через Ra, Rb, Rc
и Rd радиусы описанных окружностей треугольников DAB, ABC, BCD, CDA.
Докажите, что неравенство Ra < Rb < Rc < Rd
выполняется тогда и только тогда,
когда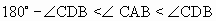 
3. Четырехугольник ABCD описан около окружности, лучи BA и CD
пересекаются в точке E, лучи BC и AD — в точке F. Вписанная окружность
треугольника, образованного прямыми AB, CD и биссектрисой угла B, касается прямой
AB в точке K, а вписанная окружность треугольника, образованного прямыми AD,
BC и биссектрисой угла B, касается прямой BC в точке L. Докажите, что прямые
KL, AC и EF пересекаются в одной точке.
4. Дан правильный 17-угольник A1...A17. Докажите, что
треугольники, образованные прямыми A1A4, A2A10,
A13A14 и A2A3, A4A6,
A14A15, равны.
Второй день.
5. На окружности отметили n точек. Оказалось, что среди треугольников
с вершинами в этих точках ровно половина остроугольных. Найдите все значения n,
при которых это возможно.
6. Дан треугольник ABC такой, что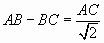 
.
Пусть M — середина
стороны AC, а N — основание биссектрисы угла B. Докажите, что
.
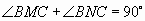7. Даны две пересекающиеся окружности с центрами O1, O2.
Постройте окружность, касающуюся одной из них внешним, а другой внутренним образом,
центр которой удален от прямой O1O2 на наибольшее расстояние.
8. Дан вписанный четырехугольник ABCD.
Известно, что четыре окружности, каждая из которых касается его диагоналей и
описанной окружности изнутри, равны. Верно ли, что ABCD квадрат?
10 класс.
Первый день.
1. Пусть a, b, c — длины сторон произвольного треугольника;
p — полупериметр; r — радиус вписанной окружности. Докажите неравенство
.
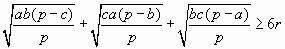2. Дан четырёхугольник ABCD. Его противоположные стороны AB и CD
пересекаются в точке K. Его диагонали пересекаются в точке L. Известно, что прямая KL
проходит через центр тяжести четырјхугольника ABCD. Докажите, что
ABCD — трапеция.
3. Радиусы описанной и вписанной окружностей треугольника
ABC равны R и r; O, I — центры этих окружностей. Внешняя биссектриса угла
C пересекает AB в точке P. Точка Q — проекция точки P на прямую OI. Найдите
расстояние OQ.
4. Через вершины треугольника ABC проводятся три произвольные
параллельные прямые da, db, dc.
Прямые, симметричные da, db, dc относительно
BC, CA, AB соответственно, образуют треугольник XYZ. Найдите
геометрическое место центров вписанных окружностей таких треугольников.
Второй день.
5. В треугольник ABC вписан ромб CKLN так, что точка L лежит на
стороне AB, точка N — на стороне AC, точка K — на стороне BC.
Пусть O1, O2 и O —
центры описанных окружностей треугольников ACL, BCL и ABC соответственно.
Пусть P — точка пересечения описанных окружностей треугольников ANL и BKL,
отличная от L. Докажите, что точки O1, O2, O и P лежат на одной окружности.
6. В треугольнике ABC M — точка пересечения медиан, I — центр
вписанной окружности, A1 и B1 — точки касания этой окружности со сторонами BC
и AC, G — точка пересечения прямых AA1 и BB1.
Докажите, что угол CGI прямой
тогда и только тогда, когда GM || AB.
7. Дано множество точек O, A1, A2 ... An
на плоскости. Расстояние между
любыми двумя из этих точек является квадратным корнем из натурального числа.
Докажите, что существуют такие векторы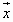 
и
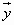, что для любой точки Ai выполняется
равенство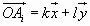 
, где k и l — некоторые целые числа.
8. Можно ли вписать правильный октаэдр в правильный додекаэдр так,
чтобы каждая вершина октаэдра была вершиной додекаэдра?
